Contributed by Tiberius Lowang
I. Preview
The adjusted Dave Male-Female Attraction Equation states that:
where:
- FA is the strength of the mutual attraction between the two people
- AM is the attractiveness of the male
- AF is the attractiveness of the female
- d is the magnitude of the societal pressure to keep the two people apart
- M is the Mutual Attraction Constant equal to 0.1
- Symbol kis defined as
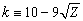where Z is the fraction of Asianness.
II. Attraction Potential
After determining the force of attraction between males and females, the next step is to find out the potential energy between the couples to further evaluate the likelihood of a relationship. Attraction potential is also an useful tool to find out if the existing relationship is stable enough to resist external stimuli such as seductions by “whores”, “hoes”, playboys, and philanderers.
By definition, the change in the attraction potential energy associated with a given displacement is defined as the negative work done by the attraction force during that displacement, or
Taking Ui at 0 and di at infinity, we obtain the equation
The potential attraction energy is negative since the force is attractive and we have taken the potential energy as zero when the couple separation is infinity. The absolute value of the potential energy is therefore the binding energy of the system.
U is also related to the probability that the relationship will start and the success of the relationship in the long run. Therefore, if you are a male trying to get into a relationship with a female, you would be more likely to be able to date her if U was higher than the female’s Choosiness Potential Threshold (CPT).
| CP Threshold | Description |
|---|---|
| 1 | Prostitute |
| 15 | Ugly girl |
| 45 | Average girl |
| 100 | Pretty girl |
| 225 | Lucy Liu / Maggie Cheung / Zhang Ziyi |
Examples:
Average Joe and Average Jane
- AF = 5
- AM = 5
- d = 1
- kM = 1
Applying the formula, we get |U| = 25. From Dave’s equation, Jane’s CT is 20 so she happily accepts Joe. However, Jane’s CPT is 45. This means their relationship probably wouldn’t last long.
Average Wang and Average Jane
- AF = 5
- AM = 5
- d = 3 (Different ethnicities + Wang makes more money)
- kM = 0.1
Applying the formula, we get |U| = 0.833. Damn! As usual, Jane rejects Wang with a vengeance and probably obtains a restraining order as well. Readers may think Asians are potent (no pun intended) even if the Force is against them. Wrong! We’re still shafted.
Bruce Lee and Average Jane
- AF = 5
- AM = 200 (Bruce kicks lots of ass)
- d = 3 (Different ethnicities + Bruce makes more money)
- kM = 0.2205 (Bruce is 3/4 Asian)
Applying the formula, we get |U| = 73.5. Looks like Bruce would have no problem getting a pretty girl. Unfortunately, potential doesn’t define reality. There are many other variables that could prevent their relationship from working out. Baseline: pray that she doesn’t meet a white person.
Horse and Average Jane
- AF = 5
- AM = 10 (he’s a nice looking horse)
- d = 104 (Different species + Horse doesn’t make much money + 15 year age difference)
- kM = 1 (Are horses from Asia? Probably not. I wouldn’t know.)
Applying the formula, we get |U| = 0.48. It’s safe to say this relationship wouldn’t work out. It also makes sense that the value is higher because there are fetishists out there with the potential to make it work. However, it’s still very unlikely.
III. Escape Velocity
Escape velocity, from a sociological perspective, measures how easy it is for a girl to withdraw from the existing relationship or to be seduced by an external stimuli. The equation is:
Low escape velocity indicates it’s extremely easy for the girl to make up her mind to leave the guy. It’s thus not surprising that the attractiveness of the girl is irrelevant here. In fact, a supermodel has the same escape velocity as a fat girl. Only the attractiveness of the male is responsible for the ability to hold the relationship together.
Now let’s reanalyze the different scenarios:
| Scenario | Escape Velocity |
|---|---|
| Joe & Jane | 3.162 |
| Wang & Jane | 0.577 |
| Bruce & Jane | 5.422 |
| Horse & Jane | 0.438 |
Evidently, it’s much easier for Jane to break up with Wang than with Joe.
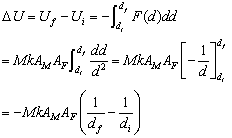
Comments on this entry are closed.